Estimating the value of Pi using Monte Carlo Method

The very first moment I was shown this, I was amazed. Estimating something using random events is pretty amazing. The first time I did this in MATLAB, but now, I think I will attempt to do the same in JavaScript.

The undelying concept of Monte Carlo Method is to use randomness to determine the value. The method is often used to solve problems that are hard to determine exactly, when there is enough statistical data available.

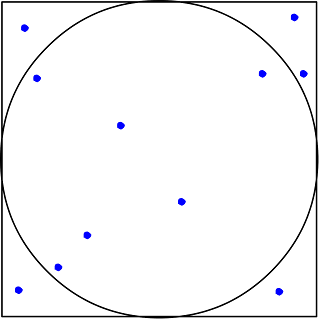
Let us define a square centered at the origin with side of length 2. A circle centered at the origin is inscribed in this square.

The assumption that we are using in this method is that if we randomly take a few points within the square, the ratio of the number of points that falls within the circle to the total points taken is equal to that of the area of the square and the circle. That is,

Area of square / area of circle = totalRandomSamples / totalPointsInCircle

Let us write a JavaScript program that could do perform this with a huge number of random sample points generated on the go. To check if the generated point lies within the circle or not, we use pythogoras theorem to calculate the distance from the center.

var squareSide = 2;
var circleRadius = squareSide/2; 

var totalRandomSamples = 100000;
var totalPointsInCircle = 0; 

for(var i = 0; i < totalRandomSamples; i++){
    // A random point contained within the square
    var newX = Math.random() * squareSide - squareSide/2;
    var newY = Math.random() * squareSide - squareSide/2;
    // Check if the new coordinate is inside or outside the circle
    if(Math.sqrt(newX * newX + newY * newY) < circleRadius){
        totalPointsInCircle++;
    }
} 

// Area of square / area of circle = totalRandomSamples / totalPointsInCircle
// (squareSide * squareSide) / (pi * circleRadius * circleRadius) = totalRandomSamples / totalPointsInCircle
var pi = squareSide * squareSide * totalPointsInCircle / (circleRadius * circleRadius * totalRandomSamples); 

console.log(pi);

The value of 𝜋 calculated using the method may vary everytime one runs the code. If you wish to improve the accurace, you can increase the number of Random Samples being used. Also, a better algorithm for generating random points may also be used.

I find that the value calculated is usually within 1% accuracy. The fact that this method simply uses cartesian coordinates to calculate 𝜋 is something that blew my mind.